Движение тел с переменной массой.
|
Константин
Эдуардович Циолковский (1857-1935).
Русский ученый и изобретатель в области аэродинамики, основоположник
космонавтики |
Характерным проявлением выполнения закона сохранения
импульса является движение тел с переменной массой и реактивное движение.
Применив закон сохранения импульса для описания движения тел с переменной массой,
К. Э. Циолковский
сделал теоретические расчеты, послужившие основой для реализации запусков
космических аппаратов. Он получил уравнение движения ракеты, происходящего за
счет выброса из нее продуктов сгорания топлива. |
Пусть в результате этого процесса за время dt скорость ракеты изменится на величину dυ, а ее масса m
уменьшится на dm. Тогда изменение импульса системы
"ракета, топливо" можно рассчитать с помощью соотношения :
dp = ((m -
dm)·(υ + dυ) + dm·u) - m·υ,
где u -
скорость выброса топлива относительно Земли;
υ - скорость движения ракеты относительно
Земли.
Согласно закону преобразования скоростей, запишем
следующее векторное равенство:
u = υт + υ,
где υт - скорость выброса
топлива относительно ракеты.
Из уравнений (14), (15) получим формулу для расчета
изменения импульса системы за время dt.
dp
= m·dυ + υт·dm.
Согласно второму закону Ньютона скорость изменения
импульса равна равнодействующей внешних сил F, действующих на систему.
Проведя разделение переменных, преобразуем уравнение
(16) к виду:
dυ= -υт·dm/m.
Проведя интегрирование (17) по скорости от 0 до υ и массе от m0 до m,
получим формулу
Циолковского (18), позволяющую
рассчитать скорость ракеты в зависимости от соотношения масс ракеты с топливом
в начальный m0 и текущий m моменты времени
и скорости истечения продуктов сгорания топлива относительно ракеты:
υ = υт·ln (m0/m).
Формулу (18) можно привести к виду, позволяющему
определить, каково должно быть отношение массы ракеты с топливом к массе
корпуса ракеты mк
для достижения ракетой заданной скорости υ,
например, первой космической.
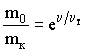 .
.
